Applications of optimization are everywhere, from the pure mathematics seen in my other research, to industry uses in operations or engineering design. But when the cost function is highly non-analytical or derived from a simulation, traditional methods of gradient-based approaches fail to be robust. Cost functions may have extremely long evaluation times, making many approaches prohibitive, especially if the optimization manifold is non-stationary and an answer is desired within a given operational window. Lastly, global optimization for multi-modal functions always presents interesting challenges to overcome. My research deals precisely in the domain where all of these problems are present. Developing new approaches to high dimensional gradient-free stochastic optimization on constrained multi-modal functions is my expertise, and I have developed an extensive software package (soon to be announced!) that contains the body of my work in this area for licensed commercial and academic use.

What does it mean for two networks to ‘connect’? If you have separate networks, whether they be networks of commerce, distribution networks, or social networks, is there a ‘naturally best’ network that connects them? Can we design a minimal system that generates such a network, and using this tool, can we then better serve the needs of our networks–creating optimal pathways to connect people, places, and ideas?

These questions are at the heart of my ongoing research, building off my network gravity framework and implementing the theoretical technology on real-world problems.

What are the fundamental building blocks of the universe, and how to they fit together to weave the fabric of space-time? Is there something natural about the fact that we live in a 3+1 dimensional universe? What dynamics exist at the interface between space-time and the empty state? These are all questions that I attempt to make rigorous progress towards answering using a novel construction that I’ve developed for studying emergent geometry from the combinatorial bulk. With some early successes, there are still numerous open questions that my framework can probe, and this research is very much ongoing.

These questions are at the heart of my ongoing research, building off my network gravity framework and implementing the theoretical technology on real-world problems.

These combinatorial objects are about as far away from smooth manifolds as you can go while still retaining some semblance of discrete geometry. I use them extensively in my emergent geometry research, and in the course of this work, I needed methods of sampling on certain spaces of these complexes. Creating Markov chains on this space with good conductance or strong ergodic sampling properties is extremely difficult due to their constrained nature, and developing, characterizing, and implementing algorithms to walk through this space is part of my ongoing research.

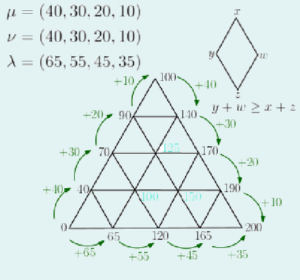
These extremely cool mathematical objects are solutions to a highly non-trivial integer linear program. They have applications throughout representation theory, but also random geometry, matrix ensembles, and combinatorics. I study methods of generating hive solutions, both in relaxed and integer cases, through Riemannian optimization methods and through constrained random walks. I also develop estimation algorithms for counting distinct hive solutions, a process that yields an important combinatorial number called a Littlewood-Richardson coefficient.

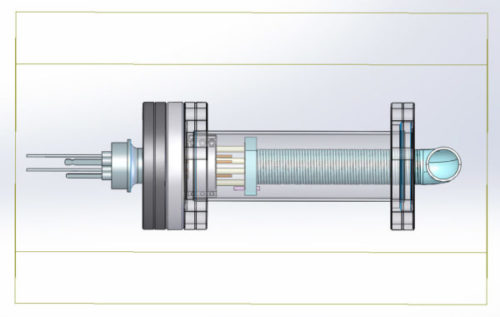
My undergraduate research was in the Vengalattore Group in the Laboratory of Atomic and Solid State Physics at Cornell. We created some of the coldest temperatures in the universe in order to study an exotic form of matter known as a Bose-Einstein Condensate. My work involved the engineering design, simulation, construction, and implementation of a variety of critical laboratory components for studying Lithium based condensates as a new atomic species of interest, creating hardware from frequency locked laser systems to a Zeeman slower.